4E1402, Marindesign och 4E1132, Lättviktsdesign Projektdokument, grupp Styrbord Lars Viebke och Benny Sjöbeck

Utvärderingsdokument 04-10-07                                           Version 1.0

 

Kite + segel

Två varianter av lösning med kite och segel behandlas här.

 

Koncept 1

Se figur 1 nedan.

Kiten är infäst så att angreppspunkten för dess dragkraft på centerbordet befinner sig nedanför angreppspunkten för resultanten av reaktionskrafterna från vattnet. Då ger kiten ett moment som vill kränga båten åt babord. För att kompensera för detta moment och för att ge ytterligare dragkraft har båten även en mast med segel alternativt en fast vinge, som alltså ger ett motverkande moment åt styrbord.

”Pontonerna” på sidorna är avsedda att kompensera för jämviktsstörningar i framförallt accelerationsfasen, då krafterna från kite och segel kan vara ojämna.

 

 

 

 

 

 

                                                                        

                                                                                   

 

 

 

 

 

 

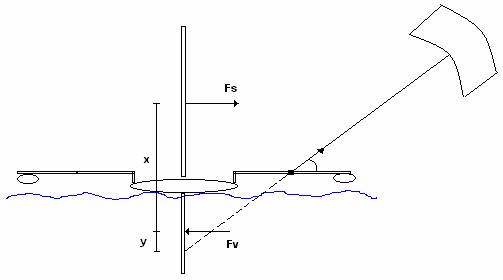
Figur 1. Vy akterifrån.

 

Fs = sidkraft från segel

Fk = dragkraft från kite

Fv = reaktionskraft på centerbord från vattnet

 

1. Krafter från kite

Kiten antas dra med en kraft, Fk, i en vinkel  från horisontalplanet och en vinkel  från ett plan tvärs båtens längsriktning, se figur 2 och 3 nedan.

 

                                         F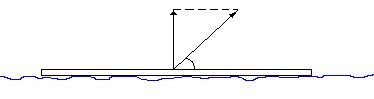_L

                                                                Fk

 

                                                   

 

Figur 2. Sidvy

 

 

 

 

4E1402, Marindesign och 4E1132, Lättviktsdesign Projektdokument, grupp Styrbord Lars Viebke och Benny Sjöbeck

Utvärderingsdokument                              2(5) 04-10-07                                           Version 1.0

 

                              

                                          

 

 

                                  

 

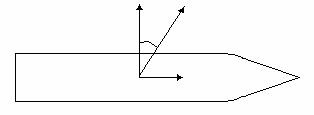
Figur 3. Vy från ovan

 

2. Momentjämvikt i sidled

Sidkrafterna från kite respektive segel måste ge lika stora men motriktade moment om båten skall gå genom vattnet utan att kränga.

Ur figur 1 erhålls då följande styrande ekvation (moment kring centerbordets mittpunkt):

 

                                                                                                   (1)

 

Ex. 1.

Antag att x = 4y och att

x = 1200 mm

y = 300 mm

Fs = 550 N  (enl. exempel från ”Optimal kurs” av Fredrik och Joel)

 

 

 för jämvikt.                                                                                                        (2)

 

OBS! Bärplan som genererar negativ lyftkraft krävs – annars flyger båten!

 

 

Ex. 2.

X, y,  och  som i exempel 1

F_L = 100 N  (max kraft utan att båten lättar från vattnet)

 

 

 

 

4E1402, Marindesign och 4E1132, Lättviktsdesign Projektdokument, grupp Styrbord Lars Viebke och Benny Sjöbeck

Utvärderingsdokument                              3(5) 04-10-07                                           Version 1.0

 

3. Dragkraft

Dragkraft från segel och kite summeras för att erhålla den totala dragkraften. Styrande ekvation:

 

                                                                                    (3)

 

Enligt ex. 1 ovan (bärplan krävs):

 

Dragkraft från segel  = 245 N enl. exempel från ”Optimal kurs” av Fredrik och Joel.

 

 

 

Enligt ex. 2 ovan:

 

 

4. Skrovmotstånd

4E1402, Marindesign och 4E1132, Lättviktsdesign Projektdokument, grupp Styrbord Lars Viebke och Benny Sjöbeck

Utvärderingsdokument                              4(5) 04-10-07                                           Version 1.0

Koncept 2

Se figur 4.

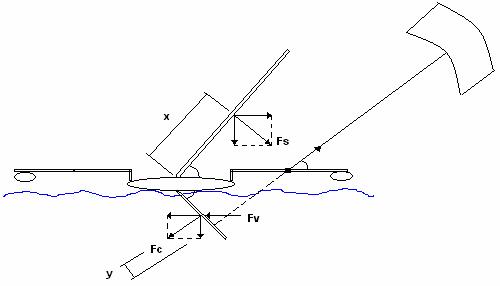
Denna lösning med lutande segel ger en nedåtriktad kraftkomposant som motverkar kitens lyftkraft. Dessutom är centerbordet utformat som en vinge, vilket ger en kraft som också den har en nedåtriktad kraftkomposant. På så vis kan dragkraften från kiten ökas utan att båten lyfter från vattnet med ett planande skrov utan bärplan. Båtens egentyngd har inte beaktats i jämviktsberäkningarna.

 

 

 

 

 

 

 

                                                                                        

                                                                                

 

                                                      

 

 

 

 

 

Figur 4. Vy akterifrån.

 

 

1. Momentjämvikt i sidled

Sidkrafterna från kite, centerbord och segel måste tillsammans ge ett nollmoment om båten skall gå genom vattnet utan att kränga.

Ur figur 4 erhålls då följande styrande ekvation (moment kring centerbordets mittpunkt):

 

             (samma uttryck som för koncept 1 ovan)                   (4)

 

2. Kraftjämvikt

Vertikal kraftjämvikt måste råda. Antag för enkelhets skull att mastens, centerbordets och kite-linans vinklar alla är samma ( i figuren), och att. Detta ger ekvationen

 

                                                                                                (5)

 

4E1402, Marindesign och 4E1132, Lättviktsdesign Projektdokument, grupp Styrbord Lars Viebke och Benny Sjöbeck

Utvärderingsdokument                              5(5) 04-10-07                                           Version 1.0

(4) och (5) ger tillsammans

 

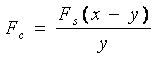                                                                                                      (6)

                                                                                                        (7)

 

 

Ex. 1

Antag att y = 300 mm som i koncept 1 ovan, men att x nu är något kortare, säg x = 1000 mm.

Vidare antas liksom i exempel 1 för koncept 1:

 

Fs = 550 N  (enl. exempel från ”Optimal kurs” av Fredrik och Joel)